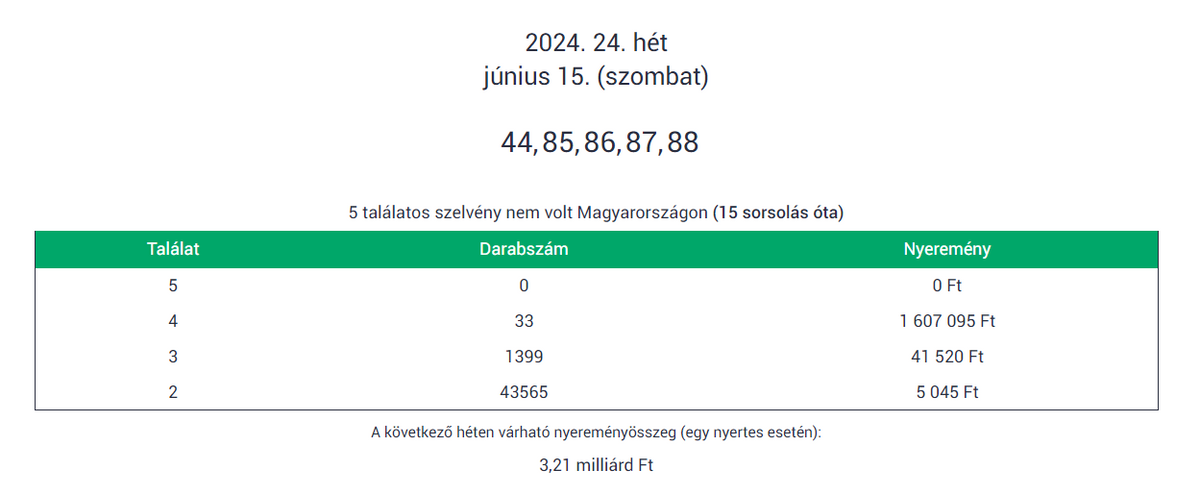
Az ötöslottón június 15-én a következő nyerőszámokat húzták ki: 44, 85, 86, 87, 88. Ilyen még nem volt! Négy egymás utáni szám!
Nyitókép: Szerencsejáték Zrt.
Mint ismert: az ötöslottón június 15-én a következő nyerőszámokat húzták ki: 44, 85, 86, 87, 88.
Ilyen még nem volt! Négy egymás utáni szám!
A Magyar Tudományos Akadémia viszont arra hívja fel a figyelmet ennek kapcsán, hogy a médiában számtalan tudománytalan állítás jelent meg egy ilyen szériának a kicsiny valószínűségéről.
„Ahhoz, hogy bizonyítsuk, hogy ez a valószínűség nem is oly kicsiny, már az emelt szintű matematika érettségin követelménynek számító valószínűségszámítási ismeretek is elegendőek: ezek birtokában könnyedén cáfolhatjuk a széles körben terjesztett hibás állításokat” – írják.
Az akadémia megjegyzi: a Wikipédián is azonnal megtalálható, hogy a lehetséges lottóhúzások száma 43 949 268. Ez a szám pedig úgy kapható meg, hogy az első számgolyót 90-ből húzzák, a következőt a maradó 89-ből és így tovább, ez 90x89x88x87x86 lehetőség. Igen ám, de a végeredmény szempontjából közömbös, hogy milyen sorrendben húzták ki a számokat, ezért ezt el kell osztani az öt szám lehetséges sorrendjeinek számával, ami 5x4x3x2.
Az most a kérdés, hogy a közel 44 millió lehetséges eredmény között hány olyan akad, ami négy egymás utáni számot tartalmaz.
Érdemes két esetet megkülönböztetni: amikor a szólóban levő szám kisebb a négyesfogathoz tartozó számoknál, illetve, amikor nagyobb náluk” – magyarázza a tudományos intézmény.
Ha a szólóban levő szám az 1-es, akkor a négyesfogat lehet 3, 4, 5, 6 vagy 4, 5, 6, 7 stb. egészen 87, 88, 89, 90-ig – ez összesen 85 lehetőség.
Ha a szingli szám a 2-es, akkor eggyel csökken a lehetőségek száma, hiszen kiesik a 3, 4, 5, 6 (mert ekkor nem négy, hanem öt egymásutáni számmal találkoznánk). Vagyis ekkor 84 lehetőség van.
Ahogy növekszik a szóló szám, úgy csökken a lehetséges négyes sorozatoké, míg végül a 85-ös után már csak egyetlen lehetőség marad: 87, 88, 89, 90. Tehát abban az esetben, amikor a szingli szám megelőzi a négyesfogatot, az összes lehetőségek száma 85+84+83+…+2+1, azaz a számok összege 1-től 85-ig.
A Magyar Tudományos Akadémia elárulja:
a legenda szerint Gauss matematikai tehetségének első megnyilvánulása volt, amikor az iskolai órán gyorsan összeadta a számokat 1-től 100-ig.
Rájött ugyanis arra, hogy ha az összeg dupláját veszi és minden számot a kiegészítő párjával ad össze, akkor (1+100)+(2+99)+(3+98)+…+(99+2)+(100+1)=100x101, tehát 1+2+3+…99+100=100x101/2=5050.
„Nekünk viszont csak 85-ig kell összegeznünk a számokat, az eredmény hasonlóan kapható: 85x86/2=3655” – összegzi az intézmény, majd hozzáteszi, hogy ne feledkezzünk meg a második esetről, amikor a szólóban levő szám nagyobb, mint a négy egymást követő!
Mint írják: ez az eset ugyanis az előzőnek a tükörképe, tehát ezeknek a lehetőségeknek a száma is 3655.
„Összegezve, azt kapjuk, hogy azoknak a lehetséges lottóhúzásoknak a száma, amikor négy egymást követő szám van (de nem mind az öt szám áll egymás után): 7310, ami az összes lehetőség 7310/43949268 része, ami körülbelül 0,0166%. Ez egy kicsi szám, de nem annyira picurka, mint amit a különböző médiatudósításokban olvasni lehetett.
Másképpen úgy interpretálható, hogy átlagosan 6012 húzásonként várható egy ilyen eredmény”
– szögezik le.
Tekintettel arra, hogy Magyarországon az ötöslottó első húzása, 1957. március 7. óta ez volt a 3511. sorsolás, nem is látszik már annyira valószínűtlennek egy ilyen eredmény.
„Kicsit haladottabb matematikai tudással az is kiszámítható, hogy 44,2% annak a valószínűsége, hogy az eddigi sorsolások során legalább egyszer találkozzunk négy egymás utáni nyerőszámmal.
Ennek fényében nem is olyan nagy csoda a szombati eredmény.
Ha valakinek akad más megoldása, várjuk kommentben! Köszönjük Pálfy Péter Pálnak, az MTA rendes tagjának!” – zárj a sorait az MTA.
A Nemzeti Közszolgálati Egyetem elindította Nemeskürty István Tanárképző Karát, amelyhez első, országosan is kiemelt gyakorlóiskoláját is megtalálta: az Óbudai Árpád Gimnáziumot, amelynek tantestülete nagy többséggel támogatta az NKE fenntartásába kerülést. Nánay Mihály rektori megbízottal, a gimnázium életében kiemelkedő szerepet játszó tanárral a fenntartóváltást érő kritikákról és a tervekről beszélgettünk.
Gulyás Balázs, a HUN-REN Magyar Kutatási Hálózat elnöke szerint a kutatási hálózat átalakításáról szóló javaslat széles kőrű támogatást élvez.
Freund Tamás elhatárolódott minden olyan kijelentéstől, amely arra utalt, hogy az egyetem polgárainak szakmai munkáját azok politikai nézetei és közéleti szerepvállalása alapján minősíti.
Rögtön az első sorsoláson telitalálat volt.
A Napi Mázli mától elérhető az értékesítőpontokon.
Nem egyeznek a vélemények arról, mi épüljön Rákosrendezőn.
Jelentős változások zajlottak le Ukrajnában az elmúlt tizenegy évben.
Argentína különutas elnöke Donald Trump bejelentése után néhány nappal közölte: komolyan foglalkozik a gondolattal, hogy kiléptesse országát a párizsi klímamegállapodásból. Ha ez megtörténne, végveszélybe sodorhatja az EU és a Mercosur-államok közötti szabadkereskedelmi megállapodást is.
